Sorting Algorithms 비교

주어진 수열을 정렬하는 알고리즘은 selection, insertion, bubble, merge, quick, heap 등 매우 다양한 방법으로 구현되어 있다.
정렬 알고리즘을 선택할 때는 stable한지, 시간 복잡도는 어떻게 되는지 등을 고려해서 선택해야 한다.

stable한 정렬이란, 입력 순서가 정렬 후에도 유지되는 정렬을 의미한다. 예를 들어 [1, 6a, 2, 6b, 4] 를 정렬한다고 했을 때, stable한 정렬은 [1, 2, 4, 6a, 6b]로 정렬된다. 즉 같은 key값을 가진 데이터의 순서가 정렬 이후에도 그대로인 것을 뜻한다.

많이 알려진 정렬 알고리즘의 시간 복잡도는 대부분 O(nlogn) 또는 O(n^2)의 시간 복잡도를 갖는다. merge, quick, heap 정렬의 경우 O(nlogn), selection, insertion, bubble 정렬은 O(n^2)의 시간복잡도를 갖는다. 특정 조건이 성립할 경우 linear sorting도 가능하지만 많이 사용되지 않는다고 한다. Python에서 제공하는 리스트의 sort 메소드의 경우 merge sort를 보완한 TIm sort를 사용하며 이 정렬 방법은 stable 정렬이며 시간복잡도도 O(nlogn)으로 빠르다.

1. Insertion Sort (삽입 정렬)

def insertion_sort(arr):                 # arr is an input list to be sorted
    for i in range(1, len(arr)):         # from 2nd to last index of arr
        key = arr[i]                     # key is the value to compare
        j = i-1                          # compare the key with the left values one by one
        
        while j >= 0 and arr[j] > key:   # if the comparing value is bigger than the key
            arr[j + 1] = arr[j]          # copy the value to the next index
            j -= 1                       # j = j - 1
        arr[j + 1] = key                 # insert key

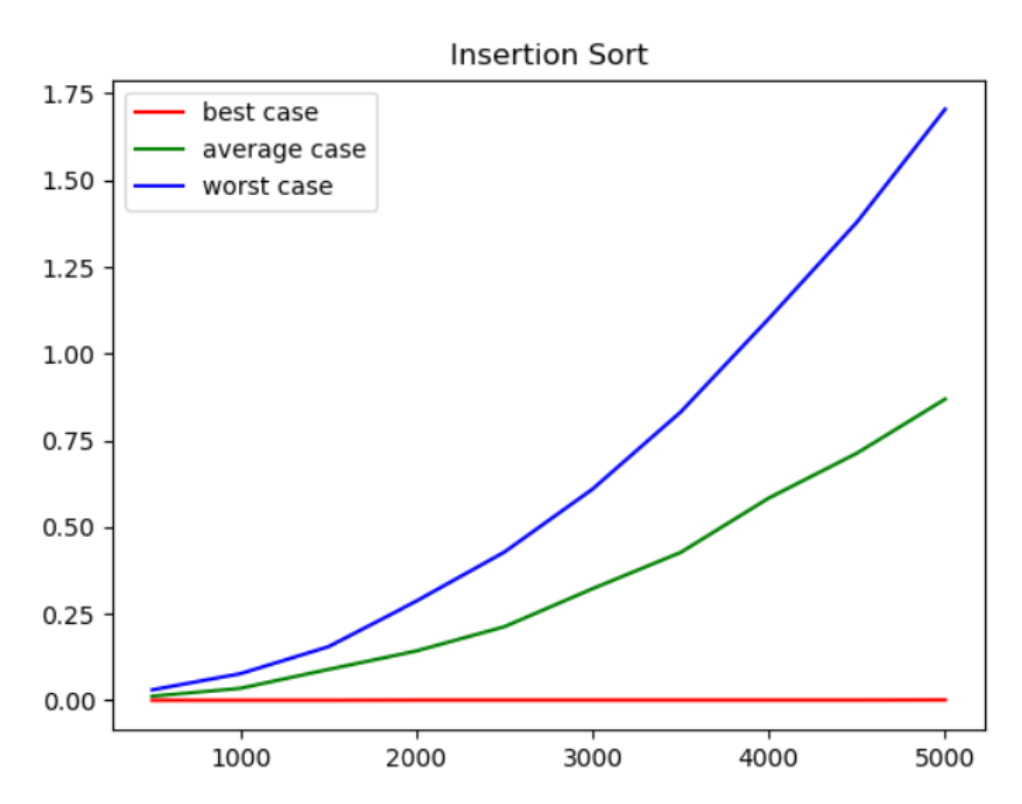
삽입 정렬 알고리즘은 다양한 정렬 알고리즘 중 구현이 매우 단순한 알고리즘으로, 위 구현 코드를 보면 매우 짧은 것을 알 수 있다. 삽입 정렬은 리스트의 1번 인덱스부터 key로 두고 key 이전의 값들을 비교하며 key의 정렬된 위치를 찾게 된다.

위 코드에서 “ j = i – 1 ”은 key가 된 인덱스의 왼쪽, 즉 작은 값부터 비교를 시작하게 된다는 의미이다. 반복문은 j가 0보다 크거나 같고, j에 해당하는 값이 key보다 크면 위치 조정이 실행된다. 첫번째 조건 j >= 0은 배열의 영역을 벗어나지 않게 해주며 두번째 조건은 정렬을 해야 하는 경우, 즉 key보다 왼쪽에 있는 값이 더 큰 값이라 위치가 변경되어야 할 경우이다.

두 조건이 만족된 경우, key보다 큰 값을 그 바로 오른쪽에 복사한 뒤, j를 1 감소시켜 계속해서 왼쪽으로 이동하며 정렬을 수행한다. 만약 반복문이 종료된 경우, 즉 배열의 맨 앞까지 정렬을 완료했거나 key가 비교 대상보다 더 큰 경우 j + 1 인덱 스에 key 값을 넣어주며 정렬을 마친다. 이 때 j + 1인 이유는 j가 비교하는 대상이 되기 때문이다. 또한 key가 비교대상보다 더 큰 경우 정렬이 종료되는 이유는 key값을 기준으로 왼쪽은 이미 정렬된 상태이기 때문이다.

2. Merge Sort (병합 정렬)

def merge_sort(x):                        # x is a list to be sorted
    if len(x) > 1:                        # if the length of x is bigger than 1
        left = x[:math.ceil(len(x)/2)]              # separate the x to two lists. the left one is 'left'
        right = x[math.ceil(len(x)/2):]             # the right one is 'right'
        left = merge_sort(left)           # sort left recursively
        right = merge_sort(right)         # sort right recursively
        return merge(left, right)         # return a list which is merged by left and right lists
    return x                              # return x if length of x is 1
    
    
def merge(x, y):                           # x is a left list, y is a right list
        temp = []                              # temp is a list to save merged list
    
        while len(x) > 0 and len(y) > 0:       # repeat until one of the lists' length is 0
            if x[0] >= y[0]:                   # if x[0] is equal or bigger than y[0]
                temp.append(y[0])              # add y[0] to temp list
                del y[0]                       # then delete the value from the y list
            else:
                temp.append(x[0])              # add x[0] to temp list
                del x[0]                       # then delete the value from the x list
            # print(temp)
        if len(x) > 0:                         # list y is done. Only list x remains
            while len(x) > 0:                  # repeat until there is no value in x
                temp.append(x[0])              # add x[0] to temp list
                del x[0]                       # delete the value
        elif len(y) > 0:                       # list x is done. Only list y remains
            while len(y) > 0:                  # repeat until there is no value in y
                temp.append(y[0])              # add y[0] to temp list
                del y[0]                       # delete the value
    
        # print(temp)
    return temp                            # return the merged list 'temp'

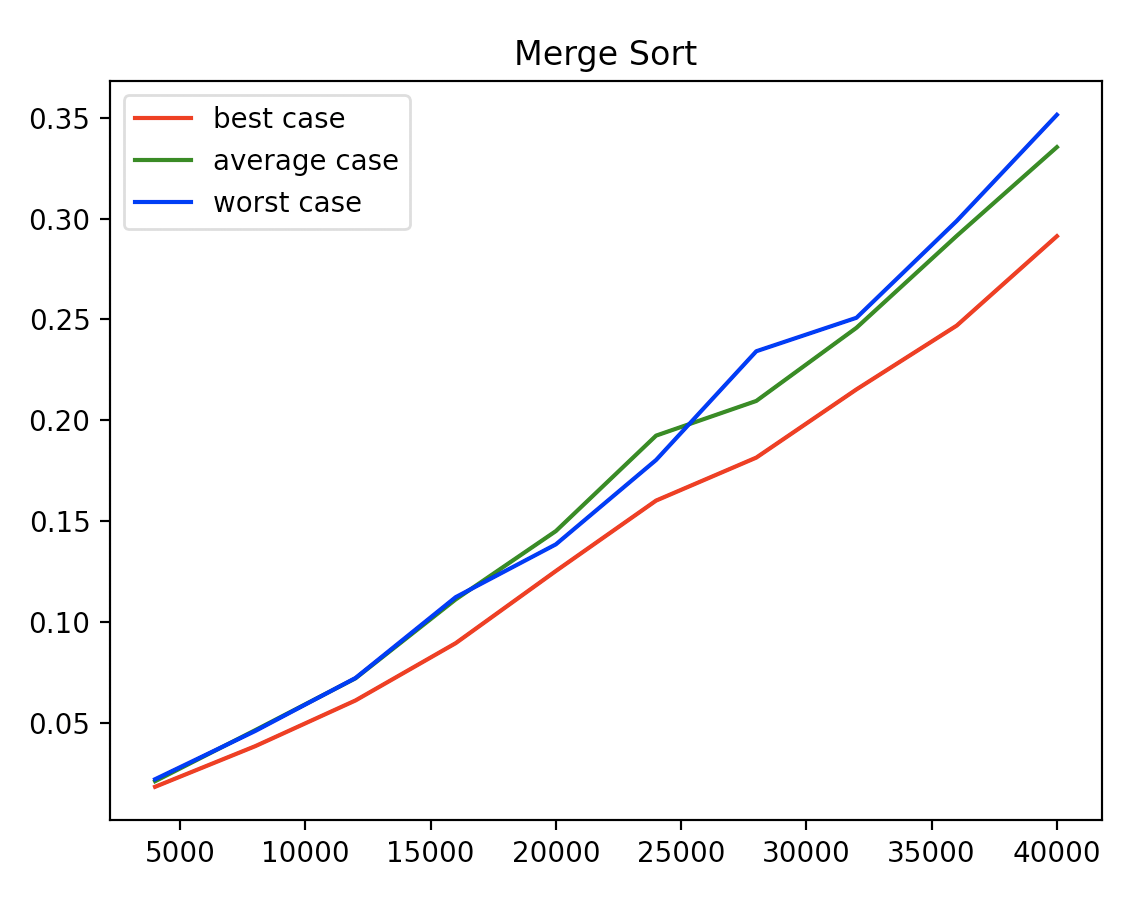
병합 정렬은 리스트를 재귀적으로 절반으로 나누어 모든 조각들의 길이가 1이 될 때 까지 분할을 진행한다. 그 후, 각 조각들의 크기를 비교하며 병합한다.

분할 조각들을 저장할 추가적인 메모리가 필요하다는 단점이 있지만, 모든 케이스에 대하여 O(nlogn)의 시간복잡도를 갖는 장점이 있다. 또한 stable sort이기 때문에 입력 순서가 바뀌지 않는다.

4. Quick Sort (퀵 정렬)

def quick_sort(list):
    if len(list) <= 1:
        return list
    pivot = list[len(list) // 2]
    left, mid, right = [], [], []
    for i in list:
        if i < pivot:
            left.append(i)
        elif i > pivot:
            right.append(i)
        else:
            mid.append(i)
    return quick_sort(left) + mid + quick_sort(right)

퀵 정렬은 기준 값(pivot)을 선택하여 pivot보다 작은 값들은 왼쪽으로, 큰 값들은 오른쪽으로 이동시킨 후, 재귀 호출을 통해 정렬 된 왼쪽 리스트와 오른쪽 리스트를 병합하여 정렬을 수행하는 알고리즘이다.

퀵 정렬 역시 O(nlogn)의 시간복잡도를 갖는다. 또한 merge sort에 비해 일반적으로 빠른 퍼포먼스를 보여주기 때문에 많은 상황에서 쓰이게 된다. 하지만 worst case의 경우 O(n^2)의 시간복잡도를 보여준다. 또한 stable 정렬이 아니기 때문에 같은 값을 가진 입력은 순서가 바뀔 수 있다.